

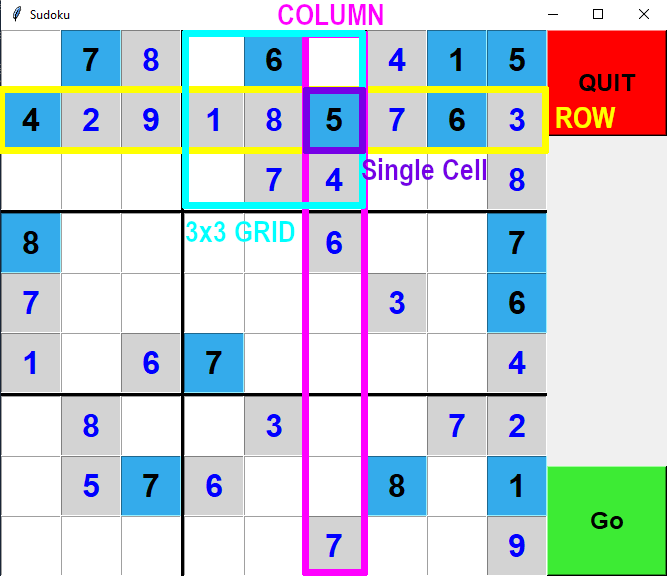
The assign function is not yet defined here. If no errors, the function returns the values dictionary back to the caller.If something goes wrong in the assign function, it returns False to signify the failure.For each square with initial digit value, we call the assign function to assign the value to the square while eliminating it from the peers.We use grid_values function to extract only relevant values (digits, ‘0’ and ‘.’).The given grid contains the initial representation of Sudoku puzzle.values are given digits as the initial value in a dictionary where each square is used as a key.values = dict((s, digits) for s in squares) for s,d in grid_values(grid).items(): if d in digits and not assign(values, s, d): return False # (Fail if we can't assign d to square s.) return values We can use the function cross to generate the 9 column units:ĭef parse_grid(grid): """Convert grid to a dict of possible values,, or return False if a contradiction is detected.""" # To start, every square can be any digit then assign values from the grid. They are 9 column units, 9 row units, and 9 box units. In total, there are 27 units on the Sudoku board. The column, the row, and the box (3x3 area) that contains square C2 are the 3 units of square C2. There are 81 squares on the Sudoku board and each square has exactly 3 units (no less, no more).įor example, the 3 units of the square C2 are shown below: The squares variable points to a list of all the 81 squares. Therefore, the function cross generates all cross products of characters from rows and cols. Peter defines digits, rows, and cols as strings.ĭef cross(A, B): "Cross product of elements in A and elements in B." return squares = cross(rows, cols) So, C2 is a square at the intersection of the third row (which is C) and the second column (which is 2). 1.1 SquaresĪ Sudoku puzzle is a grid of 81 squares the majority of enthusiasts label the columns 1–9, the rows A-I, and call a collection of nine squares (column, row, or box) a unit. It may not be obvious at first glance if you don’t know what squares and units are. Peter gives a beautiful summary of its rule in one sentence.Ī puzzle is solved if the squares in each unit are filled with a permutation of the digits 1 to 9. If you are unfamiliar with Sudoku, I recommend visiting Sudoku Dragon and reading their Sudoku rule description. In some places, I changed the indentation of Peter’s code, but I did not alter his program logic. Note: the original article by Peter uses Python 2, but I’m using Python 3 in this article.
SUDOKU SOLVER PYTHON CODE
I will break down his article and explain the code step-by-step. However, some people may struggle to understand the concise code and cannot appreciate the beauty. I was impressed with his concise and beautiful Sudoku Solver Python code that solves any Sudoku puzzles systematically. The generated Sudoku grid should have enough clues (numbers in cells) to be solvable resulting in a unique solution.I recently came across Peter Norvig’s Solving Every Sudoku Puzzle.

The Backtracking approach may not always be the most effective but is used in this challenge to demonstrate how a backtracking algorithm behaves and how it can be implemented using Python.Īn extra challenge would be to design an algorithm used to create a Sudoku Grid. Note that there are other approaches that could be used to solve a Sudoku puzzle. A recursive function is a function that calls itself until a condition is met. Every time you reach a dead-end, you backtrack to try another path untill you find the exit or all path have been explored.īacktracking algorithms can be used for other types of problems such as solving a Magic Square Puzzle or a Sudoku grid.īacktracking algorithms rely on the use of a recursive function. The typical scenario where a backtracking algorithm is when you try to find your way out in a maze. Each time a path is tested, if a solution is not found, the algorithm backtracks to test another possible path and so on till a solution is found or all paths have been tested. A Sudoku puzzle is a partially completed grid, which for a well-posed puzzle has a single solution.Ī backtracking algorithm is a recursive algorithm that attempts to solve a given problem by testing all possible paths towards a solution until a solution is found. The objective of a Sudoku puzzle is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 subgrids that compose the grid (also called “boxes”) contains all of the digits from 1 to 9. The purpose of this Python challenge is to demonstrate the use of a backtracking algorithm to solve a Sudoku puzzle.


 0 kommentar(er)
0 kommentar(er)
